After The Merge │ Part 2: The Verge
1 Background & Context
In Part 1 of this series, we discussed the Surge, one of Ethereum’s four post-Merge protocol development roadmaps:
The Surge itself is focused with increasing scalability at the data availability layer in order to provide enough space for rollups to post their transaction data. If you haven’t read it already, I would recommend starting with Part 1 before continuing.
This post is to discuss another of these roadmaps: the Verge. Before we can get into what the Verge is trying to achieve, it’s useful to provide a little context around what goes into a block, what Merkle trees1 are and how they’re used for the state, and how all of that affects full nodes.
1.1 The contents of a block
This image, a visual representation of the Ethereum blockchain mechanism, by Lee Thomas, provides a detailed view of what actually goes into a block. The ‘block contents’ portion of the image is shown below:
As we can see, the block header of a block contains a lot of crucial information. Most of it is not relevant when it comes to the Verge, but it’s still useful for our general understanding to highlight a few key elements below:
parentHash – the hash of the previous block.
stateRoot – the hash of the root node of the state Merkle tree after all the transactions included in the block have been executed. This root hash encapsulates the entire state of the system: account balances, contract storage, contract code, etc.
transactionsRoot – the hash of the root node of the transactions Merkle tree, populated with each transaction in the transactions list.
receiptsRoot – the hash of the root node of the receipts Merkle tree, populated with the receipts of each transaction in the transactions list.
number - the number of that block in the blockchain, where the genesis block = 0.
timestamp – the Unix-based timestamp for when the block was created.
Alongside the block header, the block will also contain a list of the transactions being included within that block.
The developments related to the Verge are focused on the state Merkle tree, which ultimately feeds into the stateRoot element of the block header.
Before we start discussing Merkle trees though, it’s pertinent to quickly explain what ‘hashing’ is, as it’s used not only in the block header but within Merkle trees as well.
1.2 Hashing
Hashing converts an input of any size to an output of a fixed size, called a hash, by running that input through a cryptographic ‘hash function’. For example, the SHA-256 algorithm (used in the Ethereum blockchain) returns a hash value of 256-bits, or 64 hexadecimal digits. This fixed size output is crucial when considering Ethereum’s limited block sizes.
Some other useful key properties of hashes:
Deterministic: The function always produces the same hash for the same input.
Preimage resistant: It is infeasible to determine x from Hash(x).
Collision resistant: It is infeasible to find x and y where Hash(x) = Hash(y).
Avalanche effect: Changing x slightly will produce significant changes to Hash(x).
Puzzle friendliness: Even knowing Hash(x) and part of x, it is still extremely difficult to find the rest of x.
For you cryptography nerds, you can read a step-by-step breakdown of how SHA-256 works here.
1.3 Merkle trees
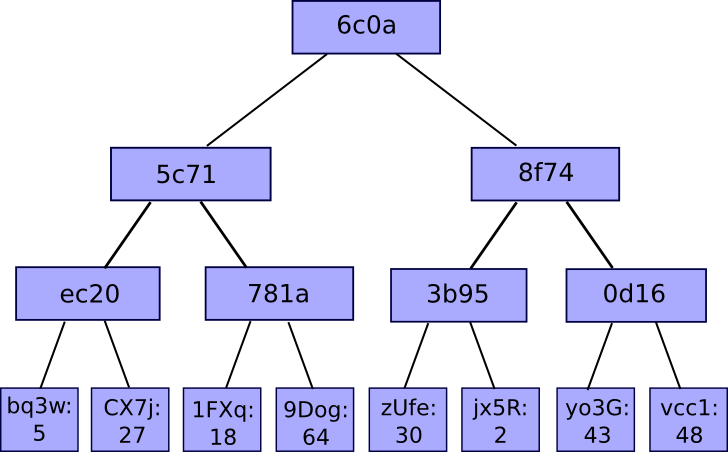
Here’s an example Merkle tree:
We start with our (unhashed) data chunks at the end of the tree - the ‘leaf’ nodes (i.e. ‘5’, ‘27’, ‘18’, etc). Individual hashes of these data chunks are then calculated (represented above by ‘bq3w’, ‘CX7j’, ‘1FXq’, etc.). Pairs of these hashes (in this particular example) are then combined and hashed again (e.g. ‘ec20’ in the case of ‘bq3w’ and ‘CX7j’) until only one hash remains - the root hash (‘6c0a’ in the image above).
Why would we do this? Why not just run the hashing algorithm on all of the eight data chunks (or their hashes) together at once (i.e. employ a completely flat hierarchy)? The answer is that using a Merkle tree structure allows for something called Merkle proofs.
1.4 Merkle proofs
Merkle proofs are there to prove that some piece of data is contained within the tree. The structure of the tree determines what information is required for the proof. With this information, anyone should then be able to easily verify this proof against the publicly available root hash.
Imagine that someone wants to prove that ‘64’ is one of the data chunks above.
If we had a completely flat hierarchy, the prover would need to provide the other seven data chunks (or their hashes) in their proof for the verifier to be able to run the hashing algorithm on everything at once and prove that it matched the root hash they already had.
With a Merkle tree structure however, far less information is required for the proof, reducing proof size.
In order to prove the presence of ‘64’, the proof now only needs hashes from three nodes to recreate the root hash, marked out in yellow:
‘1FXq’ to combine with ‘9Dog’ and be hashed in order to recreate ‘781a’.
‘ec20’ to combine with ‘781a’ and be hashed in order to recreate ‘5c71’.
‘8f74’ to combine with ‘5c71’ and be hashed in order to recreate the root hash ‘6c0a’.
These yellow nodes are known as sister nodes - all nodes in the tree that share a parent with any of the nodes in the path going down to the leaf node you are going to prove.
This efficiency of authentication can be effectively scaled up to cover large databases of data. As explained by Vitalik from a 2015 post on Merkle trees:
The application is simple: suppose that there is a large database, and that the entire contents of the database are stored in a Merkle tree where the root of the Merkle tree is publicly known and trusted (eg. it was digitally signed by enough trusted parties, or there is a lot of proof of work on it). Then, a user who wants to do a key-value lookup on the database (eg. "tell me the object in position 85273") can ask for a Merkle proof, and upon receiving the proof verify that it is correct, and therefore that the value received actually is at position 85273 in the database with that particular root. It allows a mechanism for authenticating a small amount of data, like a hash, to be extended to also authenticate large databases of potentially unbounded size.
These types of proofs, to demonstrate that some piece of data or information is contained within the tree, are also called witnesses.
1.5 The state Merkle tree
So now we know a little about how Merkle trees work in general, let’s look at the state Merkle tree, the root hash of which goes into the block header as the stateRoot.
This state Merkle tree is of a particular kind called a Merkle Patricia tree. It’s worth quickly discussing what this is first.
1.5.1 Merkle Patricia trees
The example Merkle trees shown above have been quite simple, with the underlying data chunks being collated in a simple ‘list’ format.
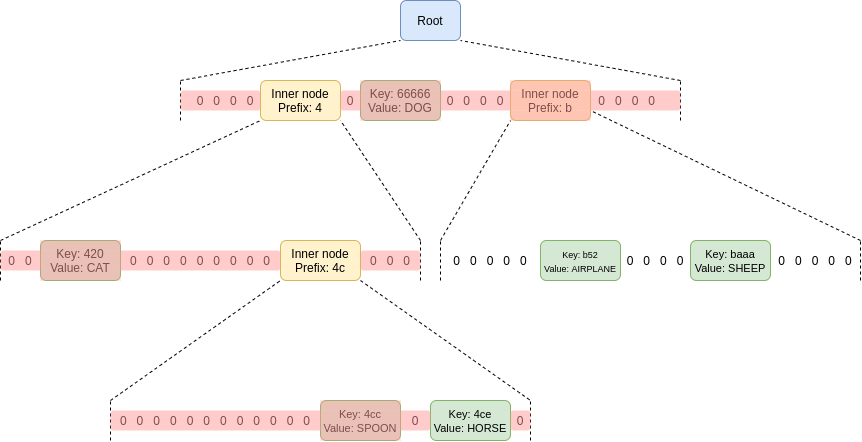
Merkle Patricia trees (also called Radix trees) instead use the properties of the underlying data chunks to determine how the tree should be structured. A trivial example of this should help clarify:
The diagram above shows how the Merkle Patricia tree is structured based on shared prefix characters from the words.
The data in the leaf nodes of the Ethereum state Merkle tree consist of key-value mappings, where the keys are Ethereum ‘0x’ addresses and the values are account balances, contract storage, contract code, etc.
As such, the state Merkle tree would use shared prefix characters from the keys (i.e. 0x addresses) to create the tree structure.
1.5.2 Updating the state Merkle tree
Whilst the transactions and receipts Merkle trees are created completely anew for every block2, there is only one global state Merkle tree which needs to update over time to reflect the changes coming from the new transactions in every block. These could be changes to existing accounts, as well as the creation of new accounts.
The Merkle Patricia tree data structure allows us to quickly calculate the new root hash in a new block after these operations, but without recomputing the entire tree, as shown in the example below:
In this simplified example, block 175224 consists only of an update to account ‘175’. Updating the stateRoot for the new block would only require a limited number of hashes from the state tree in the preceding block (those shown being connected from the old state tree to the new one). The new stateRoot, like the one in the preceding block, would still encapsulate the entire state of the system3.
Given that the stateRoot in any block N is derived using hashes from block N-1’s state Merkle tree, we should be able to work recursively to obtain an address’s key information (e.g. balances, etc.) at any prescribed block number.
Using a Merkle Patricia structure for the state tree also brings a couple of other benefits:
The depth of these trees are bounded by the maximum length of an Ethereum address (42 characters), preventing an attacker from deliberately crafting transactions to make the tree as deep as possible (simulating a denial-of-service attack) such that each individual update becomes extremely slow.
The root of the tree depends only on the data, not on the order in which updates are made. Making updates in a different order and even recomputing the tree from scratch should not change the root.
It’s worth noting that all of the example Merkle trees above show nodes having a maximum of two child nodes (i.e. ‘binary’ Merkle trees). As Ethereum addresses uses hexadecimal numbering (i.e. each address takes its 42 characters from a 16-character alphabet), the state Merkle tree (as well as the transactions & receipts trees) can have up to 16 child nodes for any given node. These trees are known as ‘hexary’ Merkle trees. (The maximum number of child nodes a parent node can have in a tree is called the width of the tree, e.g. hexary Merkle trees have a width of 16.)
This image, a visual representation of Ethereum’s modified Merkle Patricia tree system, by Lee Thomas, provides a detailed view of how the nodes in the state tree are actually categorised and how they work:
1.6 The ‘statefulness’ requirements for full nodes
Full nodes are a critical element of the consensus layer of Ethereum, and include both ‘validation’ nodes (which stake ETH) and pure ‘consensus’ nodes (which don’t). They store the full blockchain data, and are instrumental in verifying proposed transactions/blocks & subsequently updating Ethereum’s state.
As the blockchain moves from one block to the next, full nodes verify state changes by taking the previous block’s stateRoot, executing all the transactions in a block, and checking if the resulting stateRoot matches what they’ve been provided in the block header of the current block. To know if these transactions are valid, full nodes store a local copy of the state.
1.7 Bringing it all together
To summarise the key points of the above sub-sections:
Many items go into the block header of a block in Ethereum.
One of these is the stateRoot - the root hash of the state Merkle tree after all the transactions included in the block have been executed.
Merkle trees by themselves are effective at efficiently proving the presence of data within that system.
Using a Merkle Patricia tree structure for the state tree brings further benefits, such as being able to quickly calculate a new block’s root hash without recomputing the entire tree.
As part of the process of moving from one block to the next, and one stateRoot to the next, full nodes need to store a local copy of the state to ensure they can accurately validate the transactions and state changes.
Whilst using a Merkle Patricia tree structure for the state tree is indeed efficient and effective, there is an even more efficient and effective form of them that requires even fewer hashes for proofs and updates: Verkle trees.
And these Verkle trees in turn can help reduce the ‘statefulness’ requirements of Ethereum’s full nodes.
2 Verkle trees
2.1 Verkle tree structure
In terms of their structure, Verkle trees are remarkably similar to Merkle Patricia trees; the main difference being that Verkle trees tend to be much ‘wider’ in practice - let’s explain why.
Merkle Patricia trees are at their most efficient in calculating proofs when their width = 2 (i.e. when they are ‘binary’)4. This is because, as we’ve discussed before, the proof of any given leaf node consists of the entire set of sister nodes. Higher widths means including more sister nodes.
Although we’ve already seen a visual example of this above, here’s another, showing in red the sister nodes that must be in included in the proof for ‘4ce’:
(This diagram will be useful as we’ll be comparing how it looks under Verkle tree proofs later.)
Verkle trees, in contrast to Merkle Patricia trees, get shorter and shorter proofs the higher the width(!). The primary limiting factor then becomes the length of time required to create the proof if the width becomes too high. In consideration of both these factors, the Verkle tree proposed for Ethereum has a width of 256.
How is this possible?
This is because you do not need to provide any sister nodes, just the hashes on the path to the leaf node itself with a ‘little bit extra (🤏)’ (to be explained below) as the proof. This is why Verkle trees benefit from greater width and Merkle Patricia trees do not: a tree with greater width leads to shorter paths in both cases, but in a Merkle Patricia tree this effect is overwhelmed by the higher cost of needing to provide all the sister nodes per level in a proof. In a Verkle tree, that cost does not exist.
So, what’s this 🤏? Well, it can get quite technical. There are two implementations of it, which I will try to explain at a high level.
2.2 🤏as multiple additional proofs using vector commitments
Let’s return to parent nodes that have to hash the information or data from their child nodes.
Assume a hash function h that hashes a list of values (z1, z2, …, zn), and outputs C.
This output C is technically called a vector commitment and are what’s used in parent nodes in both Merkle and Verkle trees. Vector commitments in Merkle trees are simple hashes themselves and only commit to two values efficiently.
In Verkle trees however, an increased efficiency in how the vector commitment works over multiple values allows us to benefit from a special property: For a given commitment C and a value zi, it's possible to make a short proof that C is the commitment to some list where the value at the i'th position is zi.
In a Verkle proof then, this short additional proof replaces the function of the sister nodes in a Merkle Patricia proof, providing confidence that a child node really is the child at a given position of its parent node. It is visualised below:
So we can say, with this first implementation, a Verkle proof requires just the hashes on the path to the leaf node itself plus a few short additional proofs to link each commitment in the path to the next.
2.3. 🤏as a single additional proof using a polynomial commitment
Vector commitments are hashes of a discrete list. Polynomial commitments, meanwhile, are hashes of polynomials, and make a proof for the evaluation of the hashed polynomial at any point.
So now we can say, with this second implementation using the extra properties of polynomial commitments, instead of requiring an additional proof for each commitment along the path, a Verkle proof requires just the hashes on the path to the leaf node itself plus a single fixed-size additional proof that proves all parent-child links between all commitments along the paths from each leaf node to the root. Powerful stuff.
It is visualised below:
This implementation allows proof sizes to decrease by 20-30x compared to the hexary Merkle Patricia trees that Ethereum uses today, and is the one being proposed for the Verge development roadmap itself.
Vitalik’s post on Verkle trees delves more into the maths behind these additional proofs.
3 Statelessness
3.1 Weak statelessness with Verkle proofs
Verkle proofs, with their significantly smaller size, are intended to be implemented in a way which removes the ‘statefulness’ requirements in Ethereum’s verifying full nodes. How so?
Well, Ethereum is aiming for weak statelessness, whereby storing the state locally is no longer required by full nodes to validate a block, but it is required by full nodes which build the block5.
Remember from Part 1 of this series that, as a result of proposer-builder separation, builders will likely be specialised already with more powerful hardware than that used by standard full nodes, meaning that they should be well suited to handle both the size of the state and its growth over time.
Following the implementation of Verkle trees, builders will now use the state to generate Verkle proofs for the parts of the state being read or affected by the transactions in that block.
These proofs, which prove the values of the state that have been accessed by the builder, will be included in the block. The verifying full node, in processing the block, should be able to verify that the state changes are valid and correct by using these Verkle proofs to recreate the stateRoot from the block header.
3.2 Implications
There are numerous implications from the validating full node perspective with this move to weak statelessness:
The requirement to store a local copy of the state disappears, and with it a (currently) 1 TB space hardware requirement.
Enabling full nodes to validate the network primarily with RAM will likely increase validator decentralisation.
Bandwidth requirements will increase a little as Verkle proof data is now also being included in the blocks, but due to significantly smaller proof sizes when using Verkle proofs (compared to Merkle Patricia proofs), this should not be too onerous.
Furthermore, weak statelessness allows Ethereum to loosen self-imposed constraints on its execution throughput with state bloat becoming less of a concern. This could lead to increased gas limits.
3.3 Implementation
Moving to Verkle trees and weak statelessness in and of itself is going to be a significantly complicated task, primarily because it will involve transitioning the state tree in-place using temporary overlay trees.
This transition can be simplified through implementing state expiry at the same time. State expiry removes state that has not been recently accessed (e.g. in the previous year), and requires witnesses (i.e. Merkle/Verkle proofs) to revive the expired state. As stated in Part 1, historical storage has a 1-of-N trust model: you only need one of the storers of the data to be honest in order to recover it accurately.
Implementing state expiry without Verkle trees would reduce the state that full nodes need to store locally to around ~20-50 GB but it would still require very large witness sizes for reviving the old state.
However, if both developments are implemented at the same time, they will solve the challenges of each other: state expiry involves creating a new state tree every year, allowing Verkle trees to be phased in over time without an in-place transition, and Verkle trees solve the issues with witness size.
State expiry is a key aim of the Purge development roadmap and will be discussed in more detail a future post.
4 Next time on ‘After The Merge’
Next time we’ll be covering the Purge, which aims to implement both:
history expiry - full nodes having only to download and serve only the most recent ~1 year of historical blocks, transactions and receipts/logs; and
state expiry - removes state that has not been recently accessed (i.e. in the previous year) to keep the active state size under control;
…eliminating technical debt, and reducing code complexity & storage requirements for full nodes, paving the way for more decentralisation.
Further reading
A visual interpretation of the Ethereum blockchain mechanism
A visual interpretation of the Ethereum Merkle Patricia tree system
Merkle trees
These can alternatively be called Merkle tries (trie pronounced either as ‘tree’ or ‘try’). In mathematics, a ‘tree’ is used to describe a general structure of recursive nodes (that look like the branches of a 🌳 tree), of which ‘tries’ are a specific kind optimised for data retrieval - which is important to us when interrogating or updating Ethereum’s state. Both ‘Merkle tree’ and ‘Merkle trie’ are used interchangeably in the space.
There is no need for the transactions and receipts trees to be persistent over time. They, along with the transactions list, are only required to validate the specific block those transactions are in and won’t necessarily be used again.
It should be made clear here that the whole state itself - captured by the entirety of the state Merkle tree - is not being stored in the block header, as that would be many GBs of data; only the root hash of the state Merkle tree - an output of fixed size - is being stored.
This means that the current ‘hexary’ Merkle Patricia tree structures used by Ethereum are already sub-optimal.
In comparison, strong statelessness would be where no full node requires the state. Instead, transaction senders would:
provide witnesses (i.e. Verkle proofs) that block producers can aggregate;
need to declare which accounts and storage keys they are interacting with; and
be responsible for storing portions of the state tree needed to generate witnesses for accounts that they care about.
Strong statelessness is elegant insofar that it completely moves responsibility to the users, although to maintain a good user experience in practice there would need to be some kind of protocol created to help maintain state for users that are not personally running nodes or that need to interact with some unexpected account. The challenges with making such protocols are currently significant.